2020 CCPC 秦皇岛站感想和部分题解
第一次参加 CCPC,开局不到一小时愉快地签完了 A、G、F,rank 银区偏高,然后就开始了三小时多的自闭调试,队友我分别开了 C 和 E 两题,都在出问题。最后两题调完还剩二十多分钟,K 这种傻逼题都搞不出来,最后耻辱地打铜了(之前敲错成银了🌚)。
由于第一次打比较正式的比赛,之前没有对 codeblocks 等 IDE 进行适应也是一个问题(我日常 Emacs + 大量插件,一个队友日常 VS),感觉时间上面多少吃了些亏。
A A Greeting from Qinhuangdao
签到题,取两个,都是红色,$\frac{C_r^2}{C_{r+b}^2}$ 即可,注意约分,红球少于两个则为 $0$。
C Cameraman
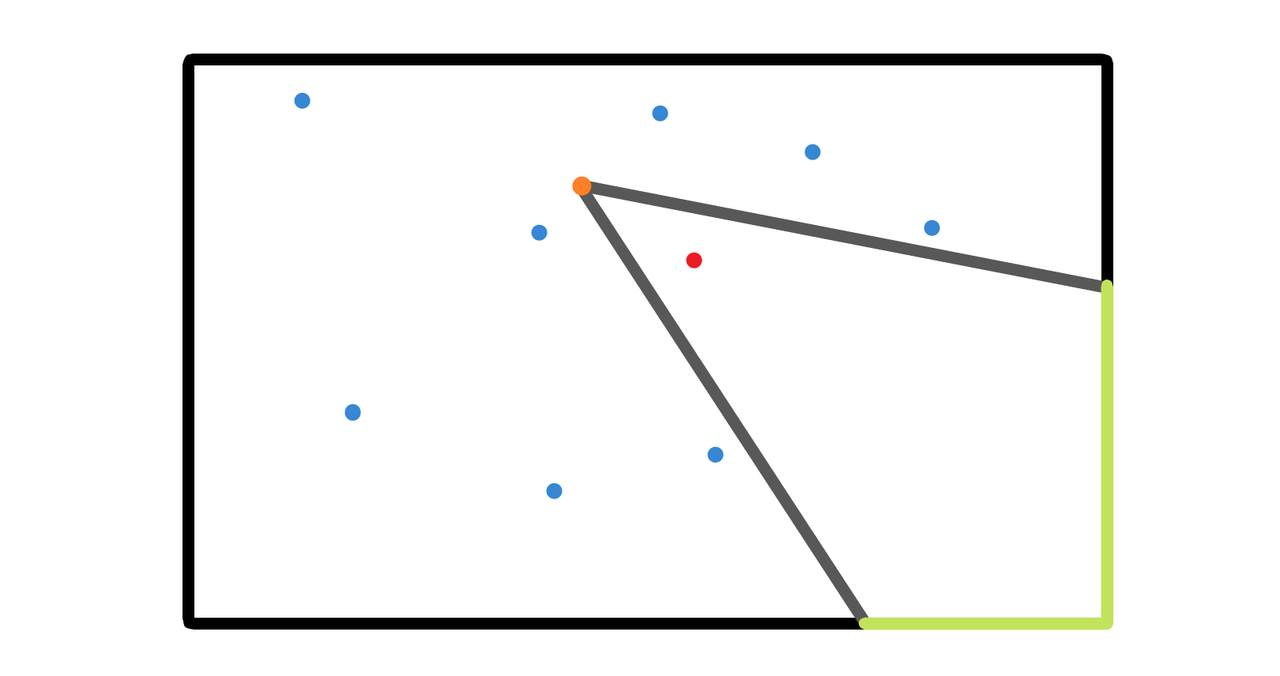
题意:Bob 的房间为矩形,长宽已知;里面有若干私人物品,Bob 自身和私人物品均视为点,位置已知固定。Alex 给 Bob 拍照,位置自选,角度范围自定(可超过 180°)。要求拍到 Bob,不拍到私人物品,求可以拍到的最大墙壁总长度。如下图绿色部分。
这题大清再次背锅,只能靠样例来猜测 Alex 和 Bob 在同一个位置时最优,否则似乎不可做。
然后,利用极角排序,找到一个方向,让直线和它两边的点紧贴,计算出结果。
由于队伍内计算几何比较薄弱,这题虽然不算难但还是在细节上出了不少问题,再加上平台上 C 题的自测是坏的(估计是因为自测没有 spj),导致比赛期间怀疑评测机有问题,浪费了大量时间。
E Exam Results
题意:有若干学生考试,每人有可能获得一高一低两个成绩(可能相等),且无法预测。本次考试的及格线为 $最高分 \times ratio$,求所有情况中,可能的最多及格人数。
对于一个人的成绩 $x$,在最高分不高于 $x/ratio$ 时,他可以及格。当然,最高分不可能低于 $x$,否则他自己的成绩将成为最高分,又因为他可能有两种成绩 $a, b$,所以当最高分位于 $[a,a/ratio]\cup[b,b/ratio]$ 时,他可以及格。
然后,我们把所有人的可能的较低分数取一个最大值,最高分至少等于它,而比它高的每个成绩也都可能作为最高分。然后枚举这个最高分,判断它在多少个人的可及格区间内,找出最大值即为答案。
数区间数量可以用线段树或者树状数组,区间更新+单点查询解决。
由于输入是百分比整数,且所有人成绩是整数,可以成绩乘 $100$(int 溢出警告)再除,向下取整作为右端点。区间范围太大,需要离散化。
本人由于在开始写代码时忘记,“所有人的可能的较低分数取一个最大值,最高分最小时就等于它”的性质,导致耗费大量时间。
F Friendly Group
题意:组内的若干学生参加学术会议。全组的友好值初始为 $0$。组内有若干对朋友,如果一对朋友同时参加,则友好值加 $1$,如果有且仅有其中一人参加,则减 $1$。最后,每个参加的人都会让友好值减 $1$。从中选择任意一部分人(可能一个都不选)参加,求可能的最高友好值。
把学生看作点,关系看作边,则友好值等于 $内部边数-跨内外边数-内部点数$。假如对于一个联通块,我们选了一部分人,那么连通块的其他部分的 $内部点数-内部点数$ 最少为 $-1$,加上它与已选部分之间的边,把整个连通块选进来结果一定不会比只选当前部分差。
因此,可以把整个连通块视为整体,用上面的公式计算,然后根据其值正负决定是否选择,最后对所有正结果取和即可得出最终结果。
G Good Number
题意:不大于 $n$ 的正整数中,有多少个可以被它的 $k$ 次方根(向下取整)整除。
对于每一个数 $i$,$[i^k,(i+1)^k)$ 开根向下取整均为 $i$,所以可以用该区间长度除以 $i$ 即可得到可被 $i$ 整除的个数。由于区间的第一个数就可被整除,所以有余数时向上取整。
由于 $n \leq 10^9$,当 $k \geq 30$ 时,所有数开根都是 $1$。
I Interstellar Hunter
题意:在一个无限制的二维空间内,Alex 一开始在原点,他会不断获得按照一个二维向量进行移动的能力,利用每个能力可以正向或反向移动无限次。询问是否可以到达特定的位置。存在多次询问,获得能力和询问可交替出现,每次询问附带价值,最后输出可到达的询问的价值之和。
对于二维向量 $\boldsymbol a$ 和 $\boldsymbol b$,利用它们能走到的位置,也就是它们的线性组合。进行变换 $\boldsymbol a = \boldsymbol a - \boldsymbol b$,它们的线性组合并不会改变。因此我们可以对它们进行辗转相除。如 $\boldsymbol a = (x_0,y_0), \boldsymbol b = (x_1,y_1)$,对其 $x$ 进行辗转相除,计算(加减乘)时使用整个向量。这样就会得到 $\boldsymbol a = (gcd(x_0,y_0), y_0’), \boldsymbol b = (0,y_1’)$ 。这样我们就可以利用询问的 $x$ 坐标轻易得出 $\boldsymbol a$ 的系数,或是不能整除直接得出不可达,然后再判断 $y$。然后出现新的向量的话,我们先将它与 $\boldsymbol a$ 进行辗转相除,使其 $x$ 为 $0$,再与 $\boldsymbol b$ 对 $y$ 辗转相除,这样它就变成无用的零向量了。
为了使当 $a$ 与新的向量进行辗转相除时在 $y$ 方向上最优,需要在 $y_0’ \geq y_1’$ 时对其相减,也就是取模。另外本题部分写法需要对 $0$ 进行特殊考虑。
K Kingdom’s Power
题意:在一个战略游戏中,地图为树形,国王在根部(点 $1$),有无限的士兵,开始全部在点 $1$。每周可以让一个军队移动到一个相邻点。求他们走一遍所有地区(可重复)至少需要的周数。
首先,对于每个非叶子节点,它都在从根节点到它对应子树的各点的必经之路上。因此只需考虑遍历所有叶子节点。
一个必然可行的方案是,对每个叶子节点,由一支军队从根部走过去。所需时间是所有叶子节点深度之和,以此作为基准值,考虑如何节省时间。
如果对某个有多个子节点的节点 $X$,如果 $X$ 的某个军队在走到了某个叶子节点 $A$ 后回来,再进入 $X$ 下面的另一个子树,则对另一个子树的某一个叶子节点来说,从根(记作 $R$,下同)到 $X$ 的路径 $d_{RX}$ 被替换为了 $d_{AX}$,节省的时间为 $d_{AX} - d_{RX}$。
对于某个节点 $X$,如果它下面的某个子树下有两个叶子节点 $A,B$,有两个军队分别从根部走到 $A,B$ 再回到 $X$,则可节省的时间为 $d_{RX} - d_{AX} + d_{RX} - d_{BX}$。此时,设 $A,B$ 的 LCA 为 $Y$,则改用如下方案:一个士兵走到 $A$ 后回到 $Y$,再进入 $B$,然后回到 $X$,则可节省的时间是 $d_{RY} - d_{AY} + d_{RX} - d_{BX}$。而 $Y$ 在 $X$ 和 $A$ 之间,$d_{AY} < d_{AX}$,$d_{RY} > d_{RX}$,后者节省的时间更多。该情况可类推到更多叶子节点的情况,从而可得到性质:对于每个子树,最多只会有一个军队从它返回到它的根节点的父节点。
然后,对于刚刚的情况,假如都要返回 $X$,则交换 $A,B$ 的位置,总的结果不变。但如果最后不返回 $X$,那么设最后的点为 $B$,设返回 $X$ 的情况下总共节省的时间为 $T$,则不返回的情况就要减去那一部分,则为 $T + d_{BX} - d_{RX}$($B$ 越深,该值越大),如果它优于 $T$,则不用返回。因此,我们在考虑子树时,把最深的放到最后,在返回父节点的情况下不影响结果,在不返回父节点的情况下结果优于其他顺序。因此,我们应在子树内计算时优先考虑较浅节点,最后把最深节点的深度用于父节点判断是否需要该子树返回。
这样我们可以对整个树进行一次 dfs,dfs 过程中判断军队是否要从当前点下面的各个子树返回到当前点。根据上一段的分析,用各子树的最深节点判断,则在 dfs 过程中获取子节点的高度(叶子为 $1$,记作 height)即可。同时传一个参数表示遍历深度(根为 $0$,记作 dep)。则对于每个子树,如果要返回,节省的时间为 $dep - height$,该值大于 $0$ 则返回,把结果减去该值。
最后,如果某节点下的所有子树都选择返回,则意味着不存在最后进入的叶子节点,这样得到的结果显然是不合理的,需要让某一个不返回。很显然,让减少的时间最少(深度最大)的一个不返回即为最优。
核心部分代码:
|
|