2020 CCPC 秦皇島站感想和部分題解
第一次參加 CCPC,開局不到一小時愉快地簽完了 A、G、F,rank 銀區偏高,然後就開始了三小時多的自閉調試,隊友我分別開了 C 和 E 兩題,都在出問題。最後兩題調完還剩二十多分鐘,K 這種傻逼題都搞不出來,最後恥辱地打銅了(之前敲錯成銀了🌚)。
由於第一次打比較正式的比賽,之前沒有對 codeblocks 等 IDE 進行適應也是一個問題(我日常 Emacs + 大量插件,一個隊友日常 VS),感覺時間上面多少喫了些虧。
A A Greeting from Qinhuangdao
簽到題,取兩個,都是紅色,$\frac{C_r^2}{C_{r+b}^2}$ 即可,注意約分,紅球少於兩個則爲 $0$。
C Cameraman
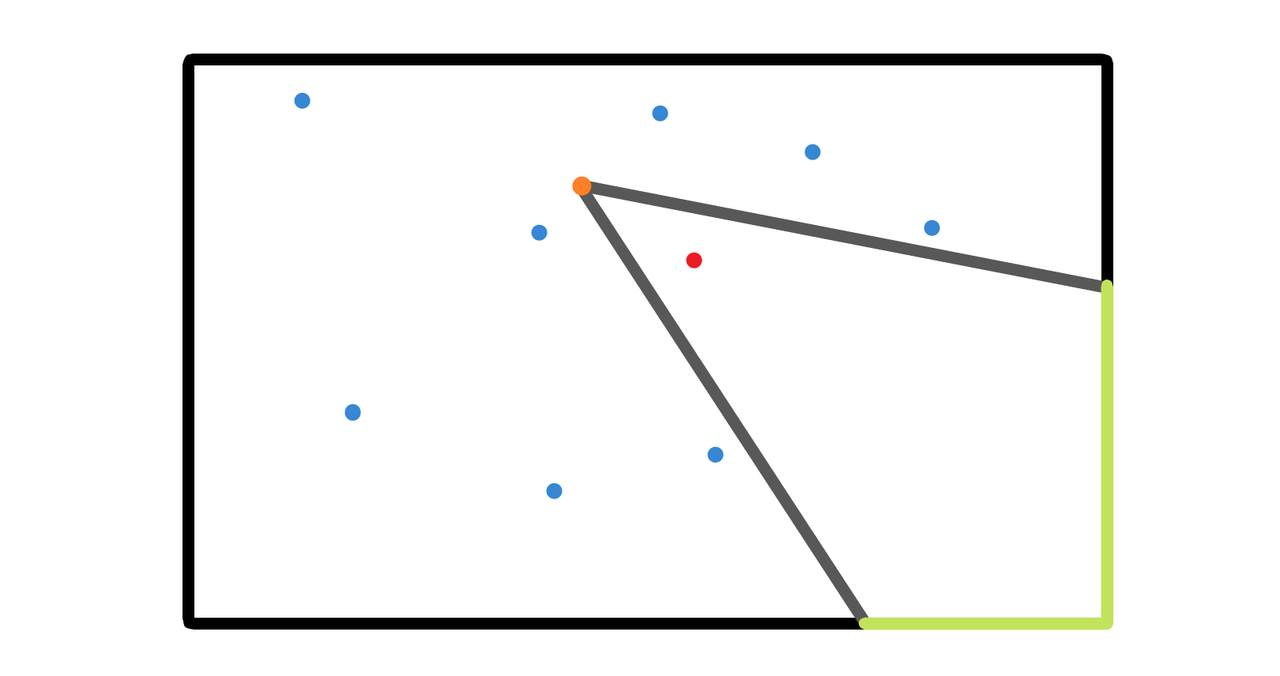
題意:Bob 的房間爲矩形,長寬已知;裏面有若干私人物品,Bob 自身和私人物品均視爲點,位置已知固定。Alex 給 Bob 拍照,位置自選,角度範圍自定(可超過 180°)。要求拍到 Bob,不拍到私人物品,求可以拍到的最大牆壁總長度。如下圖綠色部分。
這題大清再次背鍋,只能靠樣例來猜測 Alex 和 Bob 在同一個位置時最優,否則似乎不可做。
然後,利用極角排序,找到一個方向,讓直線和它兩邊的點緊貼,計算出結果。
由於隊伍內計算幾何比較薄弱,這題雖然不算難但還是在細節上出了不少問題,再加上平臺上 C 題的自測是壞的(估計是因爲自測沒有 spj),導致比賽期間懷疑評測機有問題,浪費了大量時間。
E Exam Results
題意:有若干學生考試,每人有可能獲得一高一低兩個成績(可能相等),且無法預測。本次考試的及格線爲 $最高分 \times ratio$,求所有情況中,可能的最多及格人數。
對於一個人的成績 $x$,在最高分不高於 $x/ratio$ 時,他可以及格。當然,最高分不可能低於 $x$,否則他自己的成績將成爲最高分,又因爲他可能有兩種成績 $a, b$,所以當最高分位於 $[a,a/ratio]\cup[b,b/ratio]$ 時,他可以及格。
然後,我們把所有人的可能的較低分數取一個最大值,最高分至少等於它,而比它高的每個成績也都可能作爲最高分。然後枚舉這個最高分,判斷它在多少個人的可及格區間內,找出最大值即爲答案。
數區間數量可以用線段樹或者樹狀數組,區間更新+單點查詢解決。
由於輸入是百分比整數,且所有人成績是整數,可以成績乘 $100$(int 溢出警告)再除,向下取整作爲右端點。區間範圍太大,需要離散化。
本人由於在開始寫代碼時忘記,“所有人的可能的較低分數取一個最大值,最高分最小時就等於它”的性質,導致耗費大量時間。
F Friendly Group
題意:組內的若干學生參加學術會議。全組的友好值初始爲 $0$。組內有若干對朋友,如果一對朋友同時參加,則友好值加 $1$,如果有且僅有其中一人蔘加,則減 $1$。最後,每個參加的人都會讓友好值減 $1$。從中選擇任意一部分人(可能一個都不選)參加,求可能的最高友好值。
把學生看作點,關係看作邊,則友好值等於 $內部邊數-跨內外邊數-內部點數$。假如對於一個聯通塊,我們選了一部分人,那麼連通塊的其他部分的 $內部點數-內部點數$ 最少爲 $-1$,加上它與已選部分之間的邊,把整個連通塊選進來結果一定不會比只選當前部分差。
因此,可以把整個連通塊視爲整體,用上面的公式計算,然後根據其值正負決定是否選擇,最後對所有正結果取和即可得出最終結果。
G Good Number
題意:不大於 $n$ 的正整數中,有多少個可以被它的 $k$ 次方根(向下取整)整除。
對於每一個數 $i$,$[i^k,(i+1)^k)$ 開根向下取整均爲 $i$,所以可以用該區間長度除以 $i$ 即可得到可被 $i$ 整除的個數。由於區間的第一個數就可被整除,所以有餘數時向上取整。
由於 $n \leq 10^9$,當 $k \geq 30$ 時,所有數開根都是 $1$。
I Interstellar Hunter
題意:在一個無限制的二維空間內,Alex 一開始在原點,他會不斷獲得按照一個二維向量進行移動的能力,利用每個能力可以正向或反向移動無限次。詢問是否可以到達特定的位置。存在多次詢問,獲得能力和詢問可交替出現,每次詢問附帶價值,最後輸出可到達的詢問的價值之和。
對於二維向量 $\boldsymbol a$ 和 $\boldsymbol b$,利用它們能走到的位置,也就是它們的線性組合。進行變換 $\boldsymbol a = \boldsymbol a - \boldsymbol b$,它們的線性組合並不會改變。因此我們可以對它們進行輾轉相除。如 $\boldsymbol a = (x_0,y_0), \boldsymbol b = (x_1,y_1)$,對其 $x$ 進行輾轉相除,計算(加減乘)時使用整個向量。這樣就會得到 $\boldsymbol a = (gcd(x_0,y_0), y_0’), \boldsymbol b = (0,y_1’)$ 。這樣我們就可以利用詢問的 $x$ 座標輕易得出 $\boldsymbol a$ 的係數,或是不能整除直接得出不可達,然後再判斷 $y$。然後出現新的向量的話,我們先將它與 $\boldsymbol a$ 進行輾轉相除,使其 $x$ 爲 $0$,再與 $\boldsymbol b$ 對 $y$ 輾轉相除,這樣它就變成無用的零向量了。
爲了使當 $a$ 與新的向量進行輾轉相除時在 $y$ 方向上最優,需要在 $y_0’ \geq y_1’$ 時對其相減,也就是取模。另外本題部分寫法需要對 $0$ 進行特殊考慮。
K Kingdom’s Power
題意:在一個戰略遊戲中,地圖爲樹形,國王在根部(點 $1$),有無限的士兵,開始全部在點 $1$。每週可以讓一個軍隊移動到一個相鄰點。求他們走一遍所有地區(可重複)至少需要的週數。
首先,對於每個非葉子節點,它都在從根節點到它對應子樹的各點的必經之路上。因此只需考慮遍歷所有葉子節點。
一個必然可行的方案是,對每個葉子節點,由一支軍隊從根部走過去。所需時間是所有葉子節點深度之和,以此作爲基準值,考慮如何節省時間。
如果對某個有多個子節點的節點 $X$,如果 $X$ 的某個軍隊在走到了某個葉子節點 $A$ 後回來,再進入 $X$ 下面的另一個子樹,則對另一個子樹的某一個葉子節點來說,從根(記作 $R$,下同)到 $X$ 的路徑 $d_{RX}$ 被替換爲了 $d_{AX}$,節省的時間爲 $d_{AX} - d_{RX}$。
對於某個節點 $X$,如果它下面的某個子樹下有兩個葉子節點 $A,B$,有兩個軍隊分別從根部走到 $A,B$ 再回到 $X$,則可節省的時間爲 $d_{RX} - d_{AX} + d_{RX} - d_{BX}$。此時,設 $A,B$ 的 LCA 爲 $Y$,則改用如下方案:一個士兵走到 $A$ 後回到 $Y$,再進入 $B$,然後回到 $X$,則可節省的時間是 $d_{RY} - d_{AY} + d_{RX} - d_{BX}$。而 $Y$ 在 $X$ 和 $A$ 之間,$d_{AY} < d_{AX}$,$d_{RY} > d_{RX}$,後者節省的時間更多。該情況可類推到更多葉子節點的情況,從而可得到性質:對於每個子樹,最多隻會有一個軍隊從它返回到它的根節點的父節點。
然後,對於剛剛的情況,假如都要返回 $X$,則交換 $A,B$ 的位置,總的結果不變。但如果最後不返回 $X$,那麼設最後的點爲 $B$,設返回 $X$ 的情況下總共節省的時間爲 $T$,則不返回的情況就要減去那一部分,則爲 $T + d_{BX} - d_{RX}$($B$ 越深,該值越大),如果它優於 $T$,則不用返回。因此,我們在考慮子樹時,把最深的放到最後,在返回父節點的情況下不影響結果,在不返回父節點的情況下結果優於其他順序。因此,我們應在子樹內計算時優先考慮較淺節點,最後把最深節點的深度用於父節點判斷是否需要該子樹返回。
這樣我們可以對整個樹進行一次 dfs,dfs 過程中判斷軍隊是否要從當前點下面的各個子樹返回到當前點。根據上一段的分析,用各子樹的最深節點判斷,則在 dfs 過程中獲取子節點的高度(葉子爲 $1$,記作 height)即可。同時傳一個參數表示遍歷深度(根爲 $0$,記作 dep)。則對於每個子樹,如果要返回,節省的時間爲 $dep - height$,該值大於 $0$ 則返回,把結果減去該值。
最後,如果某節點下的所有子樹都選擇返回,則意味着不存在最後進入的葉子節點,這樣得到的結果顯然是不合理的,需要讓某一個不返回。很顯然,讓減少的時間最少(深度最大)的一個不返回即爲最優。
核心部分代碼:
|
|